Laws of Logarithms
- Sean Melvein A. Vecina
- Jan 18, 2023
- 1 min read
1st law of logarithms. If a in logb (a) = c is in multiplication form, then we can expand the logarithm by adding it.
Here is an example so you can understand it further. 1. log2 (3x)
log2 (3x) = log2 3 + log2 x
2. log3 (9y) = log3 9 + log3 y
log3 (9y) = log3 3^2 + log3 y
Then we apply the 2nd principle of logarithms (logb b^x = x)
log3 (9y) = 2 + log3 y
2nd law of logarithms. If a in logb (a) = c is in division/fraction form, we can expand the logarithm by subtracting it.
Here is an example:
log3 (4/5) log3 (4/5) = log3 4 - log3 5
log3 (x/81) log3 (x/81) = log3 x - log3 81 log3 (x/81) = log3 x - log3 3^4 log3 (x/81) = log3 x - 4
3rd law of logarithms. If the logarithm contains an exponent/is carried by a number(square, cube, etc), then you must multiply the exponent to the whole logarithm.
Here is an example:
log3 (2^5) log3 (2^5) = 5log3 2
log(ab^2) log(ab^2) = log a + log b^2 log(ab^2) = log a + 2log b
Bonus Example:
ln [x(x-5)]
ln [x(x-5)] = ln x + ln (x - 5)
log [(x + 7) x] log [(x + 7) x] = log(x + 7) + log x
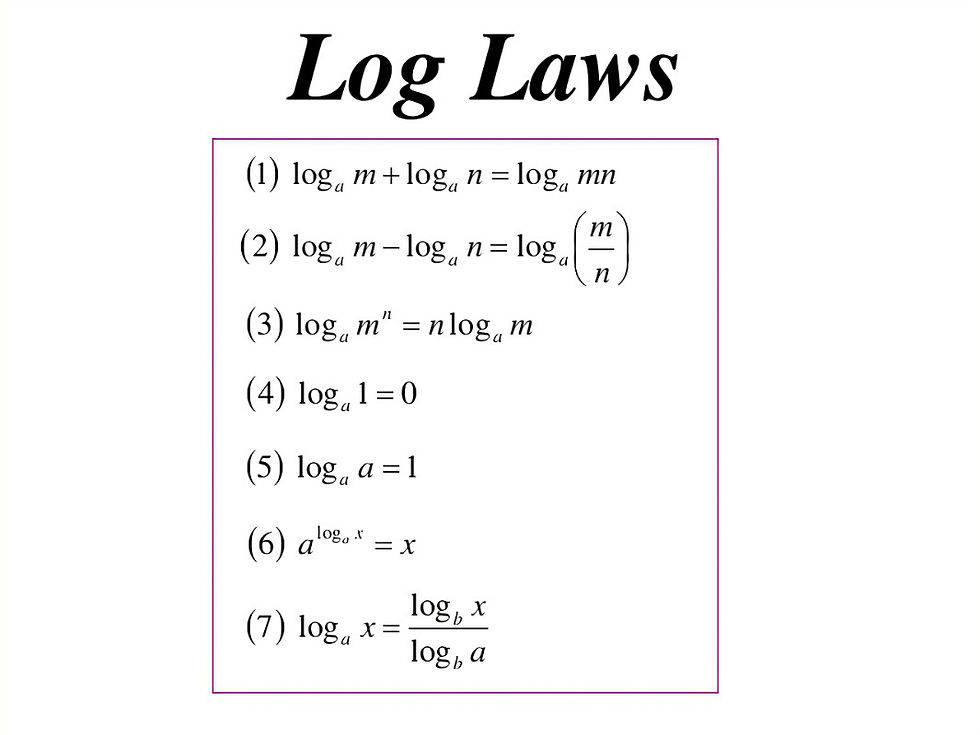




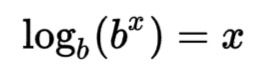
Comments