Logarithms' definition:
Let a and b be positive real numbers such that b is not equal to 1. The logarithm of a with base b is denoted by logb a (read as "log base b of a) and is defined as the number such as b^logb a = a (that is because when b^c = a, then, c = logb a). That us logb a is the exponent that b must be raised to produce a.
Here is the equation/expression:
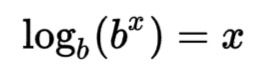
Examples of logarithmic expressions.
a. log2 32 = 5
b. log5 1= 0
c. log6 1/6 = -1
d. log5 (1/√5) = -1/2
and here is the process.
log5 (1/√5) = x
5^x = 1/√5
5^x = (√5)^-1
(5^x)^2 =(√5)^-1)^2
5^2x = 5^-1
2x = -1
2x/2 = -1/2
x = -1/2
so, log5 (1/√5) = -1/2
Logarithmic expressions/forms are the inverse function of exponential forms. Here are some examples:
Logarithmic Forms Exponential Forms
a. log2 32 = 5 2^5 = 32
b. log5 1 = 0 5^0 = 1
c. log6 1/6 = -1 6^-1 = 1/6
d. log5 (1/√5) = -1/2 5^(-1/2) = 1/√5
Types of Logarithmic Forms.
Common Logarithms are logarithms with base 10: log x is a short notation of log10 x.
Example: log 100 = 2
Natural Logarithms are logarithms with the base e (approximately 2.17828) and are denoted by "ln" in either word. In x is another way of writing loge x (log base e of x).
Example: ln 7.5 = 2.01490302
Comments