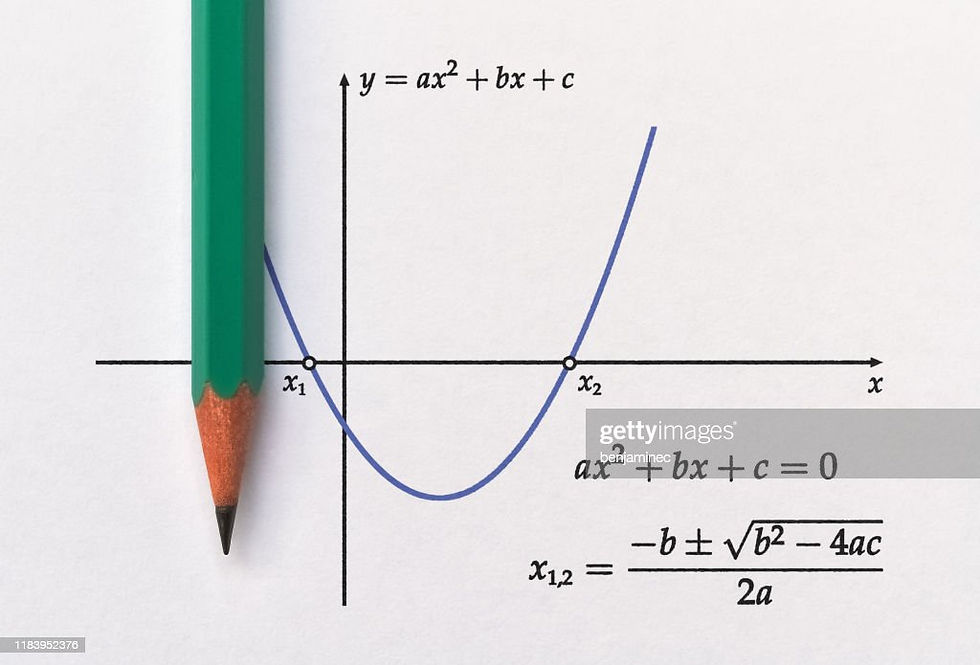
A quadratic equation is a second-order equation written as ax2 + bx + c = 0 where a, b, and c are coefficients of real numbers and a ≠ 0. Quadratic Equations are used in real-world applications. For example, if school management decides to construct a prayer hall having a carpet area of 400400 square meters with its length two-meter more than twice its breadth then to find the length and breadth we need the help of a quadratic equation. In this article, let’s discuss Quadratic Equations and their applications in detail.
A polynomial equation of degree 22, is called a quadratic equation.
A quadratic equation in the variable xx is an equation of the form ax2+bx+c=0ax2+bx+c=0, where a,b,ca,b,c are real numbers, a≠0.
Quadratic Equation Examples
Example-1: x2–6x+8=0x2–6x+8=0
It is of the form ax2+bx+c=0ax2+bx+c=0. Therefore, it is a quadratic equation.
Example-2: x+12=0x+12=0 x+12=0x+12=0.
It is not of the form ax2+bx+c=0ax2+bx+c=0. Therefore, it is not a quadratic equation.
Example-3: x2+2x+2=0x2+2x+2=0
It is of the form ax2+bx+c=0ax2+bx+c=0. Therefore, it is a quadratic equation.
What are the Roots of Quadratic Equation?
In general, a real number αα is called a root of the quadratic equation ax2+bx+c=0,a≠0ax2+bx+c=0,a≠0. If aα2+bα+c=0aα2+bα+c=0 We can say that x=αx=α is a solution of the quadratic equation. Note that the zeroes of the quadratic polynomial ax2+bx+cax2+bx+c and the roots of the quadratic equation ax2+bx+c=0ax2+bx+c=0 are the same.
If a quadratic polynomial is equated to zero it becomes a quadratic equation. The values of xx satisfying the equation are known as the roots of the quadratic equation.
What is Discriminant?
The value of (b2–4ac)(b2–4ac) in the quadratic equation ax2+bx+c=0ax2+bx+c=0. a≠0a≠0 is known as the discriminant of a quadratic equation. The discriminant of a quadratic equation indicates the nature of roots.
Nature of the Roots of Quadratic Equations
Since (b2–4ac)(b2–4ac) determines whether the quadratic equation ax2+bx+c=0ax2+bx+c=0 has real roots or not, (b2–4ac)(b2–4ac) is called the discriminant of this quadratic equation.
So, a quadratic equation ax2+bx+c=0ax2+bx+c=0 has
Two distinct real roots, if b2–4ac>0b2–4ac>0
Two equal real roots, if b2–4ac=0b2–4ac=0
No real roots, if b2–4ac<0b2–4ac<0
Quadratic Equation Formula
If b2–4ac≥0b2–4ac≥0, then the roots of the Quadratic Equation ax2+bx+c=0ax2+bx+c=0 are given by –b±b2−4ac√2a–b±b2−4ac2a. This is the formula for finding the roots of a quadratic equation and it is known as the formula for finding roots of a quadratic equation.
Solving Quadratic Equation By Factorization Method
If we can factorize αx2+bx+c,a≠0αx2+bx+c,a≠0 , into a product of two linear factors, then the roots of the quadratic equation ax2+bx+c=0ax2+bx+c=0 can be found by equating each factor to zero.
Example: Find the roots of the quadratic equation 6x2–x–2=06x2–x–2=0
Solution: We have 6x2–x–2=06x2–x–2=0
⇒6x2+3x–4x–2=0⇒6x2+3x–4x–2=0 ⇒3x(2x+1)–2(2x+1)=0⇒3x(2x+1)–2(2x+1)=0 ⇒(3x–2)(2x+1)=0⇒(3x–2)(2x+1)=0
The roots of 6x2–x–2=06x2–x–2=0 are the values of xx for which (3x–2)(2x+1)=0(3x–2)(2x+1)=0
Therefore, (3x–2)=0(3x–2)=0 or 2x+1=02x+1=0
x=23x=23, x=–12x=–12
Hence, the roots of are 23&−12
Commentaires